Étoiles de Planck : La recherche sur la gravité quantique s’aventure au-delà de l’horizon des événements

Le paradoxe de la perte d’information est un tel banc d’essai de la modélisation théorique à l’heure actuelle parce qu’il suggère que notre théorie de la physique quantique ou notre modèle des trous noirs est défectueuse ou au moins incomplète (le cas le plus probable étant les deux/et, comme c’est habituellement la solution aux paradoxes apparents, qui résulte des deux/ou pensées). De plus, et c’est peut-être le plus important, il est également reconnu avec une certaine prescience que la résolution du paradoxe de la perte d’information détiendra la clé d’une description holistique de la gravité quantique, et sera donc un progrès majeur vers une théorie unifiée des champs de la physique.

Le paradoxe, tel qu’il est formulé, découle de considérations sur le sort ultime de l’information qui tombe dans un trou noir : disparaît-elle en tombant dans la singularité au milieu ? De plus, qu’arrive-t-il à l’information d’un trou noir lorsqu’il s’évapore à cause du rayonnement Hawking (un mécanisme décrit par Hawking dans les années 70 où les trous noirs rayonnent lentement leur énergie ou masse) ? Mais pourquoi les physiciens parlent-ils d’information et que signifient-ils par là ? Il y a un certain nombre de caractéristiques qui décrivent l’état de la matière et de l’énergie, et on pense qu’il s’agit du contenu informationnel de la matière. La plupart de ces informations sont les mêmes données que celles que l’on donnerait pour décrire son propre état – comme sa position relative (où en êtes-vous ?), sa vitesse (êtes-vous en mouvement ou êtes-vous immobile ?), etc… Ces états sont donc des informations. Par conséquent, il existe une équivalence entre l’information et l’énergie. Si un trou noir perd toute son énergie, alors toute l’information sur toutes les particules qui y sont tombées serait également perdue. Bien sûr, la disparition d’informations serait une violation des lois de conservation de l’énergie, qui stipule qu’aucune énergie/information ne peut être détruite.

Nassim Haramein a toujours soutenu que le problème du paradoxe de l’information est généré artificiellement par la compréhension incomplète du rayonnement des trous noirs, dans laquelle les particules virtuelles des fluctuations du vide ne font pas qu’extraire l’énergie du trou noir, mais aussi l’alimenter en énergie ou en information dans le trou noir dans un retour continu, que nous expérimentons comme les champs gravitationnel et électromagnétique.

Les étoiles de Planck

Néanmoins, en supposant que l’évaporation des trous noirs se produise, les astrophysiques Carlo Rovelli et Francesca Vidotto ont offert peut-être l’une des solutions les plus acceptables jusqu’à présent à ce paradoxe apparent (malgré la solution des vortex de Leonard Susskind, et très probablement un progrès majeur dans notre modèle des trous noirs en général. L’équipe, dans sa publication intitulée Planck Stars, démontre comment un objet qui s’effondre gravitationnellement ne peut pas être écrasé jusqu’à un point de dimension zéro (sans blague), mais plutôt atteindre un point d’équilibre métastable lorsque le volume atteint une densité masse-énergie spécifique. Imaginez ce qui se passerait si la masse de 14 de nos Soleil était comprimée dans un espace de la taille d’un noyau atomique, quelle force serait nécessaire pour la comprimer davantage ? Selon Rovelli et Vidotto, l’équilibre est atteint puisque la force extrême de gravité vers l’intérieur est équilibrée par une puissante force répulsive de la densité d’énergie du vide quantique.

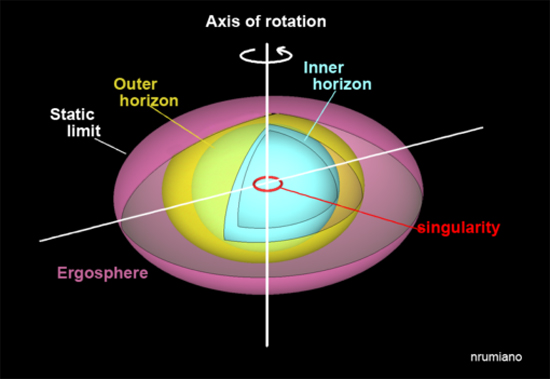
Normalement, la gravité quantique n’est décrite qu’à la taille extrêmement petite du diamètre de Planck (~10-33 cm). Comme dans la théorie de la gravité quantique en boucle, où l’espace lui-même, semblable à la structure atomique, a une quantité discrète d’espace-temps comme des filaments, tissés ensemble en réseaux de spin, dont l’évolution est appelée spinfoam. Bien que Rovelli et Vidotto utilisent principalement les valeurs de Planck, ils suggèrent que les phénomènes gravitationnels quantiques peuvent devenir pertinents à des tailles beaucoup plus grandes que planckiennes. La raison en est que, bien que le volume d’une masse qui s’effondre par gravité soit beaucoup plus grand que le diamètre de Planck, l’énergie de la densité de Planck d’un centimètre cube d’espace est extrêmement grande (~1093 grammes par centimètre cube), et puisque la pression quantique est le résultat direct de la densité énergétique – une force de répulsion quantique gravitationnelle aura lieu à une taille relativement grande pour compenser l’effet écrasant de l’affaissement gravitationnel. On prévoit que cette pression quantique se produira à des tailles proches de l’échelle subatomique (de l’ordre de 10-10 – 10-14 cm). Par conséquent, selon leurs calculs, un trou noir qui s’effondre s’arrêterait et « rebondirait » lorsqu’il atteindrait, ce qui s’avère être, la taille approximative d’un proton (un fait non mentionné par les auteurs), qui est encore d’environ 20 ordres de grandeur plus grand que la longueur du Planck. Dans la section ci-dessous, nous discuterons du formalisme utilisé par Rovelli et Vidotto qui sont des variations d’équations (volumes, surfaces, longueurs) trouvées dans l’article de Haramein intitulé Quantum Gravity and the Holographic Mass, et la relation du cadre Planck Star avec sa solution de masse protonique.

Retour vers le futur

En termes d’étoile de Planck, une masse comprimée à cette densité ne satisferait plus aux équations classiques d’Einstein (sans compter la solution holographique de Schwarzschild de Haramein) – la relativité générale rencontre une fois encore la théorie quantique. Immédiatement, certains physiciens lèveraient les mains et crieraient que cela ne pouvait pas être physiquement pertinent, car un trou noir de ce diamètre exploserait presque immédiatement dans une explosion de rayons gamma à haute énergie (à cause de la relation entre le taux de rayonnement Hawking et la taille du trou noir – plus un trou noir est petit, plus il dégage d’énergie). Cependant, ce qui est négligé dans un tel scénario (qui a été une critique qui a également été appliquée au modèle de trous noirs subatomiques de Haramein), ce sont les effets relativistes d’une masse aussi fortement compacte. On sait qu’à l’horizon des événements d’un trou noir, quelle que soit sa taille, la courbure extrême de l’espace-temps fait que les trames inertielles locales (espaces adjacents à l’horizon des événements) subissent un facteur de dilatation du temps. Ce n’est pas seulement l’espace qui se déforme et se plie sous l’effet de la gravité et de l’accélération, mais aussi le temps. Dit simplement, du point de vue d’un observateur externe, le temps semble ramper jusqu’à presque un arrêt près de l’horizon des événements d’un trou noir en raison de l’accélération approchant des vitesses relativistes, ou si vous voulez, la vitesse de la lumière.

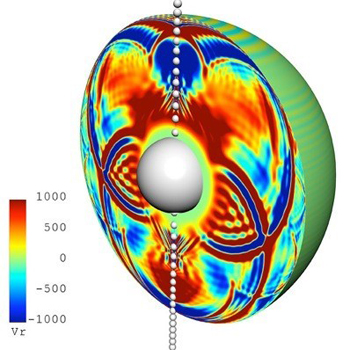
Par conséquent, le temps propre d’une étoile de Planck (le temps vécu dans le cadre de référence de l’étoile de Planck elle-même) est très court (en supposant que le rayonnement Hawking est réel), mais du point de vue d’un observateur externe, le rayonnement d’une étoile de Planck avant son « rebond » est extrêmement long. À partir de son propre horizon temporel, il s’effondre fondamentalement très près de la densité de Planck, puis subit rapidement un « rebond » dans lequel il renvoie toutes ses informations dans l’Univers – nous évitant ainsi la perte redoutée d’informations. L’équipe démontre combien de temps une étoile Planck serait autour d’un observateur extérieur. En prenant un trou noir avec une masse d’environ 1015 grammes (proche de ce qui pourrait être considéré comme un trou noir primordial, que nous décrirons bientôt), il aura un rayon d’environ 10-14 centimètres (environ le rayon du proton), alors le facteur de dilatation temporelle calculé est d’environ 14 milliards d’années – ou environ la durée pendant laquelle l’Univers est censé avoir été créé ! Par conséquent, ces objets semblent étonnamment stables. En passant, si vous pouviez survivre aux forces gravitationnelles extrêmes de la marée, entrer dans le cadre de référence d’une étoile Planck serait un voyage rapide vers le futur – vous seriez immédiatement transporté dans le futur lointain, lointain de l’évolution de cette étoile, quelque chose de cool à penser.

L’univers bébé

Or, si l’on considère l’Univers primitif, Rovelli et Vidotto démontrent qu’il n’émergeait peut-être pas d’un point de singularité comme on le croyait auparavant, mais plutôt du « rebond » d’une étoile de Planck atteignant la densité de Planck et donnant ainsi une explication alternative au Big Bang et une source d’énergie (la densité énergétique du vide) à la raison pour laquelle l’Univers est en expansion. À la densité planckienne, l’Univers était à une température si élevée que même les particules subatomiques ne pouvaient pas se former. Dans cette densité d’énergie de masse extrêmement élevée, on pense que partout dans l’Univers, de petits amas de cette soupe au plasma auraient pu s’effondrer pour former des trous noirs. Ces trous noirs sont appelés trous noirs primordiaux, et sont théoriquement susceptibles d’être répartis dans tout l’espace, même aujourd’hui, et ont probablement été les ancêtres des trous noirs supermassifs qui se trouvent au cœur de la plupart des galaxies. Puisqu’un trou noir primordial à l’échelle atomique aurait un cycle de rebond d’environ 14 milliards d’années, en utilisant les paramètres calculés par Vidotto et Rovelli pour la dilatation temporelle – certains de ces trous noirs primordiaux commenceraient tout juste maintenant à connaître leur « rebond quantique », selon notre perspective (même si dans leur temps propre il s’est passé 14 milliards d’années !). Rovelli et Vidotto suggèrent que nous pourrions être capables de détecter ces événements en interceptant des rayons gamma à haute énergie depuis l’espace. Par conséquent, selon eux, ces rayons gamma à haute énergie peuvent contenir des preuves empiriques réelles de la gravité quantique.

Le facteur Haramein

Cependant, Rovelli et Vidotto ne connaissant pas la solution holographique de Haramein ne savaient pas qu’il existe déjà des preuves empiriques de la gravité quantique. C’est que la prédiction de Haramein du rayon de protons basée sur la densité de Planck du vide, qui est à ce jour la prédiction la plus précise de la dernière mesure de protons, et qui est le seul modèle théorique (y compris le modèle standard) qui la prédit avec précision, est la preuve empirique que les fluctuations du vide quantique de Planck ont des effets réels et mesurables, notamment la formation du proton dans ce cas (voilà pourquoi Rovelli et Vidotto ont trouvé un rayon très semblable pour leur Planck Star). Haramein extrait le rayon correct du proton en démontrant que la gravité, non seulement à l’échelle quantique mais aussi à l’échelle cosmologique, est fondamentalement le résultat de la structure granulaire de l’information de Planck de l’espace-temps produisant la force gravitationnelle que nous expérimentons comme trous noirs, et l’applique à l’échelle quantique pour montrer que la force dite confinée qui lie les protons ensemble dans le noyau est en fait mal marquée comme force forte. Par conséquent, la structure des atomes eux-mêmes est une preuve empirique de la gravité quantique due aux fluctuations du vide en tant qu’acteur fondamental dans la création de notre monde, de la genèse cosmologique comme l’ont démontré Rovelli et Vidotto à la structure et aux forces de l’ensemble du monde matériel. C’est pourquoi les calculs de Planck Star les ont finalement amenés au rayon d’échelle de dans le voisinage d’un proton.

La formule utilisée par Rovelli et Vidotto est extrêmement pertinente car les équations 3, 4, 8 et 9 dans leur article sont toutes des variations de base de l’équation 19 dans la papier « Gravité quantique de Haramein et la masse holographique », donné là comme : r=2ℓ(m/mℓ) où ℓ est la longueur de Planck et mℓ est la masse de Planck…. Les deux approches sont de nature géométrique et décrivent différents aspects de la dynamique de l’espace-temps induite par la résolution quantique. Ainsi, Rovelli et Vidotto arrivent à la même formule que Haramein à partir d’un chemin complètement différent, dans leur cas la courbure, où Haramein vient de la structure holographique de pixillation discrète de l’espace-temps. Dans tous les cas, les deux sont comme les pièces d’un puzzle qui s’emboîtent pour nous donner une compréhension plus profonde de l’évolution universelle et de la création.

Pourtant, bien que l’équipe d’astrophysiciens soit arrivée à une étoile de Planck dans la région du rayon d’un proton, il ne leur est pas forcément venu à l’esprit que la densité de Planck dans ce volume lorsque le « rebond » se produirait est équivalente à la densité énergétique constante cosmologique du vide dans le reste de l’Univers, qui est actuellement considérée comme la source de l’expansion de l’Univers. Par conséquent, la stabilité apparente du proton, ou dans leur cas l’étoile de Planck, n’est pas seulement due à la dilatation temporelle, mais aussi à un état d’équilibre entre la pression gravitationnelle quantique interne de densité de Planck du proton et la densité d’énergie cosmologique du vide qui le retient.

L’utilisation des équations de Haramein de la gravité quantique et de la masse holographique, auxquelles Rovelli et Vidotto sont apparemment parvenus indépendamment, démontre la puissance de l’approche de la masse holographique pour décrire la dynamique qui implique la gravité quantique.

yogaesoteric
19 avril 2020