Géométrie sacrée : la perfection de la nature
Nombre d’or, suite de Fibonacci, fleur de vie, solides de Platon… La géométrie dite sacrée est partout autour de nous, dans le visible et l’invisible, dans l’infiniment petit comme dans l’infiniment grand. Elle a nourri l’art et l’architecture, mais c’est bien de la nature et de son observation qu’elle est née.

Comme l’a dit Albert Einstein, « Il n’y a que deux façons de vivre sa vie : l’une en faisant comme si rien n’était un miracle, l’autre en faisant comme si tout était un miracle. »
Il en va de même avec la géométrie sacrée : soit elle est partout dans la nature, soit elle n’est nulle part. De fait, elle est partout puisque c’est de l’observation de la nature que les hommes ont déduit cette géométrie : « Les cristaux, les fleurs, les fruits, les animaux, tous ont servi de modèle pour créer cette géométrie particulière », écrit Stéphane Cardinaux, architecte et chercheur en géobiologie. La nature étant considérée comme une perfection, l’être humain peut en comprendre les lois d’organisation géométrique et s’en inspirer pour ses propres créations.

Divina proportione
Que l’on tranche un concombre, un chou, que l’on considère la spirale d’une coquille de mollusque ou bien la symétrie de l’étoile de mer, les mêmes proportions vont s’exprimer, et une en particulier : la « divina proportione » de Luca Pacioli, mathématicien et moine franciscain italien du XVe siècle. Celui-ci en parlera comme d’un « trésor caché », qui renvoie à une « science secrète », car les caractéristiques de la proportion tiennent à Dieu. « Le premier est l’unicité… », écrit-il. Cette proportion divine est connue depuis Euclide selon la règle : « Une droite est dite divisée en moyenne et extrême raison quand toute la quantité est au plus grand segment comme ce dernier est au plus petit. » Si l’on bâtit un rectangle avec le long segment pour base et le court segment pour côté, on obtient un rectangle d’or.
La proportion ne prendra l’appellation de « nombre d’or » qu’au XIXe siècle, désigné par la lettre grecque φ (phi). Sa valeur est de 1,618… Il intervient dans la construction du pentagone régulier, dans certaines phyllotaxies (arrangement des feuilles d’une plante) ou encore dans le « pavage de Penrose », un modèle de structure des quasi-cristaux. C’est Johannes Kepler, vers 1600, qui va découvrir les relations entre la section dorée et les nombres de Fibonacci. La fameuse « suite de Fibonacci » est en effet très simple ; il s’agit d’ajouter les deux termes précédents pour obtenir le suivant, en partant de 0 et 1 : suivent 1, 2, 3, 5, 8, 13, 21, 34, 55…, et le rapport de deux termes consécutifs tend vers phi. La preuve que cette suite se trouve dans la nature est que Fibonacci l’a découverte en se demandant combien de paires de lapins pouvaient être « produites » par une seule paire en un an, en supposant que tous les animaux survivent. Chaque paire engendre une nouvelle paire chaque mois, et pour compter il suffit d’additionner les paires des deux mois précédents, pour arriver à 377 paires à la fin de l’année.
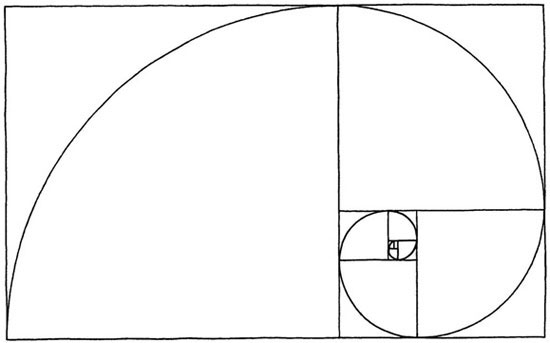
Modèle de croissance équilibrée
En 1202, Leonardo Fibonacci a écrit le Liber abaci, soit le livre du calcul, ou de l’abaque, un des premiers à introduire les chiffres arabes en Europe occidentale. Il combine cette connaissance avec ses propres réflexions. Géométriquement, la suite de Fibonacci s’exprime en une croissance de carrés de taille 1, puis 2, 3, 5, etc. En traçant dans chaque carré un quart de cercle de rayon égal au côté, on forme une spirale qui croît indéfiniment.
Contrairement à une idée reçue, la spirale logarithmique de la coquille du nautile ne repose pas sur le nombre d’or, mais c’est bien le cas de l’arrangement des graines de tournesol, des pétales de rose ou des écailles d’une pomme de pin. La géométrie sacrée du nombre d’or, même si elle n’est pas omniprésente, se trouve à toutes les échelles, puisque cette suite peut également alimenter une géométrie fractale qui génère la répétition d’objets « auto-similaires » à différentes échelles.
Selon Michael Schneider, mathématicien et auteur d’un respecté The Beginner’s Guide to Constructing the Universe, « cette séquence de nombres permet une croissance par expansion continuelle mais très équilibrée. C’est un motif de croissance expansive que l’on retrouve partout dans la nature et dans la vie organique. Aussi bien la position des branches sur certains arbres que la croissance du chou, des cornes de bouquetin ou des galaxies… La croissance de la coquille du mollusque ne modifie pas son centre de gravité, comme pour les cornes du bouquetin, et donc maintient son équilibre. » Quand la disposition de feuilles consécutives sur une tige forme un angle de 137,5° environ, correspondant à « l’angle d’or », l’arrangement global permet qu’aucune feuille ne se retrouve complètement au-dessus d’une autre, ce qui maximise à la fois la captation des rayons du soleil et de l’eau de pluie. Il faut souligner que toutes les plantes ne suivent pas ce motif de croissance, mais celles qui le font en tirent ce profit, tout comme les graines de tournesol rangées sur la fleur en utilisant le maximum de la surface.
Critères de beauté et d’harmonie
Les spirales qui s’observent dans des plantes comme le chou, l’artichaut ou le tournesol peuvent être comptées dans un sens et dans l’autre : on trouve toujours des paires de nombres de Fibonacci consécutifs comme 34 dans un sens et 55 dans l’autre, ou bien 55 et 89, ou 89 et 144, etc. Le fameux chou romanesco est quant à lui l’exemple d’une spirale fractale puisqu’on retrouve le même motif aux différentes échelles. Le nombre d’or permet également de construire le pentagone régulier et l’étoile qui en est issue, le pentagramme. On le retrouve dans la pomme tranchée par le milieu, qui fait apparaître cinq loges à pépins. Ce pentagramme est un principe féminin qui symbolise Vénus, à la fois planète et déesse. Au Moyen Âge, le pentacle servait à repousser les démons, et on retrouve cette étoile sur les drapeaux américain ou européen, celui de l’islam ou de l’Union soviétique…
Selon le chirurgien californien Stephen Marquardt, la divine proportion fonde les critères de beauté d’un visage et l’harmonie entière du corps : « La distance qui sépare le nombril du sol et celle entre le nombril et la tête sont dans un rapport de proportion entre 1 et 1,618, explique-t-il. Et cela est également vrai pour d’autres parties du corps comme les segments des jambes, le haut du corps, le buste, le cou et la tête, les phalanges, etc. Au niveau du visage, la largeur de la bouche correspond à 1,618 fois celle du nez sur les visages que nous avons tendance à trouver beaux, et la largeur de la base du visage est 1,618 fois celle de la bouche. C’est valable pour le triangle du nez, de face ou de profil, et même les dentistes ont constaté que les incisives latérales sont 1,618 fois moins larges en moyenne que les incisives centrales. » Marquardt est connu pour avoir mis au point un « masque de beauté » en appliquant ces règles de proportion à toutes les parties du visage. L’astrophysicien d’origine roumaine Mario Livio a également publié un livre sur le nombre d’or et se demande dans Dieu est-il mathématicien ? comment il est possible que les développements abstraits des mathématiques finissent toujours par trouver une application. N’est-ce pas la preuve qu’elles sont tout simplement le langage de la nature ?

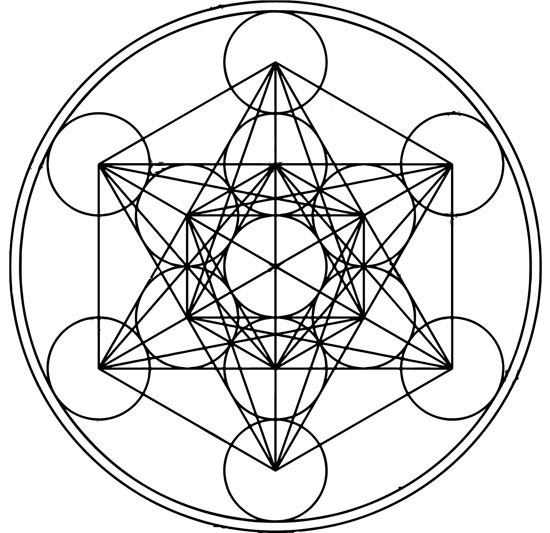
Fleur de vie : la structure du vide ?
Si l’on considère qu’un tour d’hélice d’ADN mesure 34 angströms de long sur 21 de large, ces deux nombres de Fibonacci placent le nombre d’or au cœur du vivant. On trouve également une géométrie sacrée dans les virus ou micro-organismes qui reposent sur les formes du tétraèdre, de l’hexaèdre, de l’octaèdre, de l’icosaèdre ou du dodécaèdre, soit les cinq « solides platoniciens ». Ils correspondaient aux éléments feu, terre, air, eau et éther (ou esprit) et on les déduit d’une autre forme archétypale en géométrie sacrée : la fleur de vie. Cette figure est constituée de cercles égaux juxtaposés. Sept cercles forment la graine de vie, quand la circonférence des six cercles périphériques passe par le centre du premier cercle et forme six pétales. La figure peut être complétée à l’infini, et donne une représentation bidimensionnelle du tore avec treize cercles.
Les solides de Platon se déduisent du « cube de Métatron », qui s’inscrit dans la fleur de vie. On va également lire l’arbre de vie séphirotique de la kabbale dans cette fleur de vie. C’est dire si sa symbolique est importante et c’est pourquoi cette figure se retrouve aussi bien dans le Codex Atlanticus de Léonard de Vinci que dans le temple d’Osiris à Abydos et dans l’art phénicien, assyrien, indien, etc…
Pour le chercheur Nassim Haramein, « si nous extrapolons le symbole de la fleur de vie en trois dimensions, il ressemble à des bulles agglomérées et définit la géométrie et la position de 64 tétraèdres. Cette grille pourrait être la structure du vide… On le trouve également dans la Cité interdite en Chine, gardé par les chiens Fu, qui sont les gardiens de la connaissance, et la fleur de vie est sous leurs pattes. » Les formes tétraèdre (pyramide), hexaèdre (cube) et octaèdre apparaissent toutes naturellement dans les structures cristallines. L’icosaèdre, l’octaèdre et le dodécaèdre sont présents dans des espèces de radiolaires, micro-organismes du plancton animal. Enfin, on retrouve des hexagones homothétiques et concentriques à la base du tracé des cristaux de neige, dont les formes reposent sur les racines carrées de 3 et de 2. On comprend que le mandala, reflet de la plénitude du cosmos, ait pris un tel essor à partir des traditions hindouistes et bouddhistes. Plus l’homme est capable d’observer dans l’infiniment grand et dans l’infiniment petit et plus il découvre les mêmes structures harmonieusement reproduites aux différentes échelles. Forme parfaite qui naît de la simple chute d’un caillou dans l’eau, le cercle est associé à l’ordre cosmique, au mouvement éternel et à l’origine de la vie. La constante Pi elle-même n’est guère moins magique que phi. Dans le mandala, qui signifie « cercle » en sanscrit, s’expriment les yantras, diagrammes mystiques qui entremêlent carrés et triangles, et qui sont l’équivalent graphique des mantras. Comme l’écrit Jean-François Malherbe dans Mandalas, « le mandala est à la fois un résumé de la manifestation spatiale, une image du monde, en même temps que la représentation et l’actualisation de puissances divines ; c’est aussi une image psychologique, propre à conduire celui qui la contemple à l’illumination. »
La danse des planètes.
Les orbites elliptiques des planètes, considérées depuis des points de vue particuliers et sur de longues durées, forment des figures géométriques harmonieuses, mandalas du système solaire. En traçant par exemple huit orbites superposées de la Terre et de Vénus, on obtient une fleur à cinq pétales. Certains observateurs n’ont pas manqué de noter que la danse de la Terre et de Vénus autour du Soleil était un tango.
Huit orbites terrestres correspondent à treize orbites de Vénus et à cinq « baisers » entre Vénus et la Terre au cours de cette période. S’il s’agit de nombres de Fibonacci, cela ne doit rien au hasard.
yogaesoteric
12 janvier 2019


