Scalar Waves and Free Energy

What is a “scalar wave” exactly? Scalar waves (hereafter SW) are often likened to “longitudinal” waves. Other theorists have modeled them as virtual pressure waves existing in subquantum “potentials”. The term “scalar” is often used because the hypothetical source of these waves is thought to be a “scalar field” of some kind. This means it possesses magnitude but not direction – similar to the Higgs Field for example.
There is nothing particularly controversial about longitudinal waves (hereafter LW) in general. They are a ubiquitous and well-acknowledged phenomenon in nature. Sound waves that travel through the atmosphere (or underwater) are longitudinal; as are plasma waves propagating through space (aka “Birkeland currents”).
Longitudinal waves moving through the Earth’s interior are known as “telluric currents”. They can all be thought of as pressure waves of sorts.
SW/LW are quite different from “transverse” waves. You can observe transverse waves (hereafter TW) by plucking a guitar string or watching ripples on the surface of a pond. They oscillate (vibrate, move up and down, or side-to-side) perpendicular to their arrow of propagation (directional movement). Comparatively SW/LW oscillate in the same direction as their arrow of propagation.
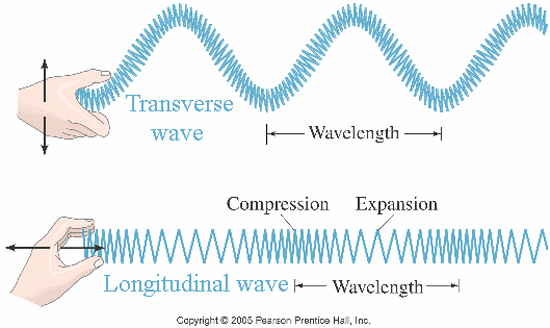
In modern day electrodynamics (both classical and quantum), electromagnetic waves traveling in “free space” (such as photons in the “vacuum”) are generally considered to be TW. But this was not always the case.
When the preeminent Mathematician James Clerk Maxwell first modeled and formalized his unified theory of electromagnetism in the late XIX Century neither the SW/LW nor the TW had been experimentally proven, but he had postulated and calculated the existence of both.
After Heinrich Hertz demonstrated experimentally the existence of transverse radio waves in 1887, theoreticians (such as Heaviside, Gibbs, and others) went about revising Maxwell’s original equations (who was now deceased and could not object). They wrote out the SW/LW component from the original equations because they felt the mathematical framework and theory should be made to agree only with experiment. Obviously, the simplified equations worked — they helped make the AC/DC electrical age engineerable. But at what expense?

Then in the 1889 Nikola Tesla (a prolific experimental physicist and inventor of AC) threw a proverbial wrench in the works when he discovered experimental proof for the elusive electric scalar/longitudinal wave. This seemed to suggest that SW/LW, opposed to TW, could propagate as pure electric waves or as pure magnetic waves. Tesla also believed these waves carried a hitherto-unknown form of excess energy he referred to as “radiant”. This intriguing and unexpected result was said to have been verified by Lord Kelvin and others soon after.
However, instead of merging their experimental results into a unified proof for Maxwell’s original equations, Tesla, Hertz, and others decided to bicker and squabble over who was “more” correct. In actuality they both derived correct results – both waveforms were now experimentally demonstrable aspects of reality. But because humans (even “rational” scientists) are fallible and prone to fits of vanity and self-aggrandizement, each side insisted dogmatically that they were right and the other side was wrong.
The issue was allegedly settled after the dawn of the 20th century when (1) the concept of the mechanical (passive-material) “Ether” was purportedly disproven by the Michelson-Morley interferometer experiments and replaced by Einstein’s relativistic space-time manifold, and (2) detection of the SW/LW proved much more difficult than initially thought – mostly due to the waveform’s subtle densities, fluctuating frequencies, and orthogonal directional flow. As a result the truncation of Maxwell’s equations was upheld.
However, it is reasonable to argue that SW/LW in free space are quite real. Beside Tesla, empirical work carried out by professional electrical engineers such as Eric Dollard, C. Monstein, Konstantin Meyl, Thomas Imlauer, and J.L. Naudin (to name only some) have clearly demonstrated their existence experimentally. These waves seem capable of exceeding the speed of light, can pass through traditional electromagnetic shielding (aka Faraday cages), and produce “over-unity” (more energy out than in) effects. As far as the evidence suggests, they seem to propagate in a yet unacknowledged “counter-spatial” dimension – perhaps outside of classical space-time.
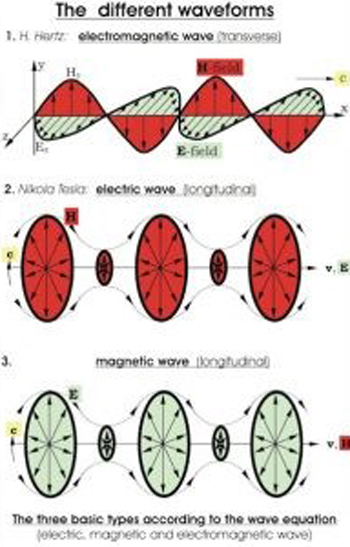
Because the concept of an all pervasive, material Ether was discarded by most scientists, the thought of vortex-like electric and/or magnetic waves existing in free space (sometimes referred to as “solitons”), without the support of a viscous medium, was thought to be impossible. However later experiments carried out by Dayton Miller, Paul Sagnac, E.W. Silvertooth, and others have contradicted the findings of Michelson & Morley. More recently Italian Mathematician-Physicist Daniele Funaro, American Physicist-Systems Theorist Paul LaViolette, and British Physicist Harold Aspden have all conceived of (and mathematically formulated) models for a free space “Ether” that is dynamic, fluctuating, self-organizing, and supports the formation & propagation of SW/LW.
Hopefully this general overview has provided you with a better understanding of scalar waves and their provocative role in scientific history.
yogaesoteric
November 24, 2018
Also available in:
 Français
Français
